RF İLKE VE BİLEŞENLERİ NEDİR ?
RF ilke ve bileşenleri nedir ? Frekans alanı nedir? RF tasarımı, analizi ve testi için frekans alanı neden bu kadar değerlidir? Bu ve benzeri sorulara cevap aradığımız RF İlke ve Bileşenlerine Giriş adlı yazımızla karşınızdayız.
RF ile ilgili teknik yazılarımıza kaldığımız yerden devam edelim.
RF İLKE & BİLEŞENLER
RF tasarımında yeterlilik kazanma sürecindeki en temel adımlardan biri belki de frekans alanında düşünmeyi öğrenmektir.Çoğumuz için, elektriksel devreler ve sinyaller ile erken tecrübemizin büyük çoğunluğu zamana göre statik veya dinamik olan gerilimler ve akımlar bağlamında kalır.
Örneğin, bir pilin voltajını bir multimetre ile ölçtüğümüzde, statik bir değere sahip oluruz ve bir osiloskopta sinüzoidal bir gerilime baktığımızda, zamanla değişen bir değere sahip oluruz.
Öte yandan RF, frekanslar dünyasıdır.Antenlere statik gerilimler göndermeyiz ve osiloskop, kablosuz iletişimde yer alan sinyal manipülasyon tiplerini yakalamak ve görselleştirmek için genellikle etkili bir araç değildir.
Gerçekten de, zaman bölgesinin de RF sistemlerinin tasarımı ve analizi için uygun bir yer olmadığını söyleyebiliriz.Farklı bir paradigmaya ihtiyacımız bulunmaktadır.
Fourier :
Fourier dönüşümü, bu alternatif paradigmaya götüren matematiksel yoldur, çünkü frekans içeriğine göre bir sinyalin tanımlanabilmesi için kesin bir yöntem sağlar.
RF bağlamında Fourier dönüşümü , son derece karmaşık sinyal varyasyonları alabilir ve bunları, orijinal frekans-alan dalga formundan çok daha bilgilendirici olan frekans-alanı bileşenlerine çevirebilir.

Fourier dönüşümü veya ayrık Fourier dönüşümü (DFT) için hesaplamaya dahil olan detaylar önemsiz değildir.Ve bu durumda endişelenmemiz gereken bir durum değildir.Temel matematiksel prosedürler hakkında çok az şey biliyor olsanız bile frekans alanlı teknikleri anlayabilir ve kullanabilirsiniz.
Fourier dönüşümü, bir sinyalin frekans içeriğini ortaya çıkaran ifadeler üretir ve DFT, karşılık gelen sayısal verileri üretir.Bununla birlikte, pratik mühendislik bağlamında, grafiksel bir ifade çoğu zaman daha uygundur.Sonunda bu frekans alanı çizimleri bir osiloskop izi kadar normal ve sezgisel hale gelir.
Spektrum
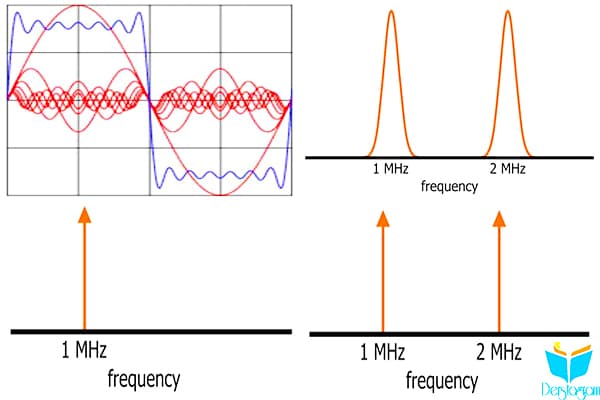
Bir frekans alanı grafiği bir spektrum olarak adlandırılır.1 MHz sinusoid için idealize edilmiş spektrum şu şekildedir: Dikey ok, 1 MHz’de belirli bir miktarda “enerji” nin bulunduğunu gösterir.
Okun çizgi kısmı çok incedir, çünkü bu idealleştirilmiş sinyal kesinlikle başka hiçbir frekans bileşenine sahip değildir – tüm enerji 1 MHz’de tam olarak yoğunlaşmıştır.
Bu mükemmel 1 MHz sinüzoidi mükemmel bir 2 MHz sinüzoid ile birleştirmek için bir toplama devresi kullansaydık, spektrum resimdeki gibi olurdu.
Bu frekans alanı grafiği, yeni sinyalin frekans karakteristikleri ile ilgili çok net veriler sağlar.Devrenizin anlık olmayan frekansla ilgili davranışıyla ilgileniyorsanız, spektrum size ihtiyacınız olan bilgiyi verir. Aksine, zaman-alan dalga biçimi basit değildir:
Bu iz, bir sinüzoidal frekans f frekansının ikinci bir sinüzoidal frekans 2f miktarına eklenmesi sonucudur.
İdeal vs Gerçek
Yukarıda gösterilen ince dikey ok frekansı bileşenleri matematiksel yapılardır ve gerçek dünya spektral ölçümleri daha çok resimdeki gibi ters ince u gibi görünmektedir.
Uyuşmazlık neden olur ?.Her şeyden önce, ölçüm sisteminin çözünürlüğü sınırlıdır ve bu sınırlamalar, orijinal sinyaldeki “ideal” nitelikler ne olursa olsun doğal olarak tehlikeye girer.Ancak sonsuz derecede hassas bir ölçüm cihazımız olsaydı bile, spektrum gürültü nedeniyle matematiksel versiyondan farklı olurdu.
Önceki bölümde gösterilen “saf” spektral bileşenleri üretebilecek tek tip sinyal mükemmel bir sinüzoittir; yani, gürültü veya periyot veya genlikte herhangi bir değişiklik yoktur.Mükemmel bir sinüzoidin özelliklerinden herhangi bir sapma, ek frekans bileşenleri getirecektir.
Sezgisel bir örnek, faz gürültüsüdür: Gerçek dünyadaki bir osilatörün her zaman aynı frekansı üretmesini beklemek pratik değildir; kaçınılmaz olarak, bir çevrimin gerçek süresinde (küçük olması umut edilir) varyasyonlar olacaktır ve buna faz gürültüsü denir.
Binlerce döngüleri kapsayan verileri toplar ve daha sonra spektral analiz yaparsanız, bu binlerce döngülü devrenin frekans içeriğini etkin bir şekilde ortalıyorsunuz demektir.Sonuç, yukarıda gösterilen spektral şekli olacaktır; dalga formunun genişliği, nominal frekanstan ortalama sapmaya karşılık gelir.
Spektral Ölçümler
Frekans alanı çizimleri, RF sistemlerini tartışmak ve analiz etmek için çok uygun bir yol sağlar. Modülasyon şemaları, parazit, harmonik bozulma — bir karalama kağıdına çizilen temel spektrumlar bile, bir durumun netleşmesine yardımcı olabilir.
Ancak, bir RF sistemini başarılı bir şekilde tasarlama zamanı geldiğinde, genellikle daha karmaşık bir şeye ihtiyacımız olacak.Daha spesifik olarak, bize spektral karakteristiği veren bir şeye ihtiyacımız vardır.
Bu, mevcut bir sistemin işlevselliğini karakterize etmek için önemlidir, ancak genellikle daha acil gereksinim, tanı ve çözümdür — yani, bu aygıt neden çalışmıyor ve bunu nasıl düzeltebiliriz.
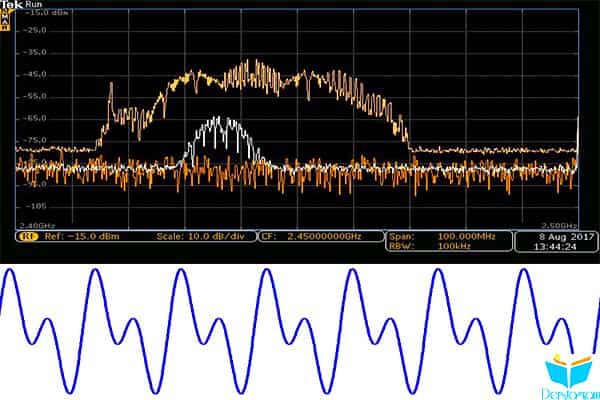
Dijital osiloskoplar “FFT” (hızlı Fourier dönüşümü) işlevselliği sunar ve bu spektral ölçümleri elde etmenin bir yoludur.Bununla birlikte, gerçek dünya frekans analizi için seçim aracı bir spektrum analizörü olarak adlandırılır.
Bu, yüksek frekanslı bir giriş sinyalini kabul etmek ve bu sinyalin frekans-alan gösterimini göstermek için özel olarak tasarlanmış bir test ekipmanı parçasıdır.Bir spektrum analizörü ile biraz pratik deneyim elde etmek, RF mühendisliğinin pratik yönlerini tanımak için önemli bir başlangıç adımıdır.
Özet :
Mühendisler, frekans etki alanı veya frekans alanı aracılığıyla elektrik sinyalleri ile etkileşime girebilir. RF bağlamında, frekans alanında çalışmak genellikle daha üretken ve sezgiseldir.
Frekans alanı analizi, RF tasarımında ve testinde genellikle çok az önem taşıyan ayrıntıları doğal olarak bastırır ve aynı zamanda odaklanmamız gereken özellikleri vurgular.
Bir frekans alanı grafiği bir spektrum olarak adlandırılır. Bir spektrum, örneğin, bir modülasyon şemasının veya girişimden kaynaklanan problemler yaşayan gerçek bir sinyalin göze çarpan özelliklerini rahatlıkla iletebilir.
Teorik spektrumlar genellikle idealize edilmiş sabit frekanslı sinüzoitlere karşılık gelen ince dikey oklardan oluşur.
Gerçek dünyadaki ölçüm ekipmanı ve gerçek dünyadaki RF sinyalleri daima daha geniş bir frekans-alan dalga formuyla sonuçlanan kusurlara tabidir.
RF tasarım laboratuvarı için gerekli bir ekipman parçası spektrum analizörüdür. Bu cihazlar, çeşitli alan analizi yeteneklerinin yanı sıra frekans alanı çizimleri de sağlar.
RF İLKE VE BİLEŞENLERİ NEDİR SONUÇ :
Bugün RF İlke ve Bileşenleri Giriş adlı yazıyı sizlerle paylaştık.Spektrum , Fourier , Spektral ölçümler gibi tanımlara ve kullanım alanlarına baktık.Umuyorum faydalı bir yazı olmuştur.
İyi Çalışmalar
