HUFFMAN ENCODING (KODLAMA) ve DECODING (KOD ÇÖZME) PROJESİ
Huffman Algoritması nedir ? Huffman Encoding & Decoding projesi nedir ? Huffman projesi ile neler yapabilirsiniz ? Matlab Proje fikirleri ile ilgili yazı dizisinin 3. yazısında Huffman encoding ve decoding projesi ile birlikteyiz.
Başlayalım.
HUFFMAN ENCODING & DECODING PROJESİ
Encoding data iletişim güvenliğinden emin olmak ve etkin şekilde bilgi taşımak için kullanılır ve önemlidir.Elektronik haberleşme sistemlerinde , Huffman algoritması popüler encoding methodudur.Karşılaşabileceğiniz geniş kullanıma sahip ana sıkıştırma yöntemlerinden birisidir.
İlgili linkte datayı encode ve decode eden bir proje göreceksiniz.Çıkış değerlerinin de veri akışı karakterlerinin entropi , verimlilik ve frekans olasılıklarını göreceksiniz.
Ek olarak bilgi vermek gerekirse ; Huffman algoritması GZIP , PKZIP(winzip etc.) ve BZIP2’den JPEG ve PNG gibi formatlara sıkıştırma yapan popüler bir methotdur.
Bazı programlar Huffman kodlama methodunu kullanırken bazılarıda tek adım , çoklu adım sıkıştırma yöntemlerini kullanmaktadır.
Huffman kodlama ve karar verme algoritması , değişken uzunluktaki kodlarla veri sıkıştırması için kullanılır.En kısa kodlar en sık kullanılan karakterlere atanır ve en uzun kodlar da en az kullanılan/seyrek kodlara atanır.
Huffman kodlaması entropi encoding algoritması ile kayıpsız data sıkıştırmayı sağlar.Entropi ise bilgi akışı içerisinde öngörülemezliğin ölçümüdür.Maksimum entropi demek toplam öngörülemeyen bitlerle ifade edilir.Kusursuz bir veri akışıda hiç entropinin olmadığı sistemdir.
Huffman kodlama methodu Shannon-Fano methodu ile benzerdir.Aralarındaki ana fark ise ; Shannon-Fano methodu kodları yukardan aşağı doğru inşa eder ve her bir bit ise soldan sağa doğru dizayn edilir.
Huffman ağaç modeli burada gösterilmiştir.Huffman algoritmasını kullanarak ‘bu huffman ağacının bir örneğidir’ cümlesi oluşturulmuştur.Kök düğümün altında , 16 ve 20 nolu yaprak düğümlerini görebilirsiniz.
Huffman algoritması ağaç yapısında , kökte 36 olduğunu varsayalım.Dallar açıldığında 16 ve 20 ile karşılaşırız.16’dan yukarı gittiğinizde 8 ve 8’i görürsünüz ve ardından 4 ve 4’ü.
Benzer şekillerde , huffman ağacının tamamını oluşturmak adına ise ; ‘a’ , ‘n’ , ‘t’ vb. ifadeler eklenmiştir.
Not : Huffman ağacı oluşumu ile ilgili daha detay bilgiler için EFY Nisan 2005’te yayımlanan ‘Veri sıkıştırma ve Dekompresyon’ yazılım projesini inceleyebilirsiniz.
En basit ağaç yapım algoritması , en düşük olasılığa veya frekansa sahip olan düğümün en yüksek önceliğe sahip olduğu öncelik sırasını veya tablosunu kullanır.
İlk olarak her sembol veya karakter için bir yaprak düğümü oluşturmalıyız ve bunu öncelik tablosuna eklemeliyiz.Tabloda eğer birden fazla düğüm var ise tablodaki en yüksek öncelikli (en düşük frekans) iki düğümü kaldırın.
Bu iki düğüm ile alt düğümler olarak ve iki düğümün olasılıklarının toplamına eşit olasılıkla yeni bir düğüm oluşturun.Son olarak tek düğüm kalana kadar bu şekilde devam ediniz.Son düğüme ulaştığınızda aslında kök’e ulaşmış olacaksınız ve ağacınız artık hazır hale gelmiş olacaktır.
Huffman Kodlamasını Kullanarak Verileri Kodlama Adımları :
1.Bir veri kümesindeki her karakterin olasılığını hesaplayınız.
2.Veri kümelerini artan düzende sıralayın.
3.En küçük frekans solda olacak şekilde ve frekanslar sırayla sağa doğru artacak şekilde sıralayınız.Ve en soldaki en küçük frekanslı ile bir sağındaki en küçük ikinci frekans için yeni bir node oluşturun.
4.Bu iki elementi listeden kaldırın ve artık bu ikisi bir nod’un parçası oldular ve olasılıkları toplayın.Yeni nod için olasılık sonucunu elde edeceksiniz.
5.Listeye sıralı ekleme işlemlerini gerçekleştirin.
6.Ardından adım 3 , 4 , 5 sıralı olacak şekilde ve tek bir nod kalıncaya kadar bu işlemi yapın.
Artık tek bir nod kaldığına göre basit bir ağaç yapısı çizebilirsiniz.
Yukarıda oluşan ağaçta sola giden her yol üzerine ‘0’ ve sağa giden her yol üzerine ‘1’ yerleştirin.Şimdi ‘0’lar ve ‘1’ler kökten başlayarak her bir sembol ya da karaktere ikili kodu(binary code) atayın.
Etkin olarak öncelik sırasındaki veri yapıları , ekleme başına O (log n) gerektirdiği için ve ‘n’ yaprakları olan bir ağacın 2n-1 düğümleri bulunduğu için , algoritma O (n log n) zamanında çalışır ki burada ‘n’ sembollerin sayıdır.
Yukarıda bulunan ifadelerden , kodlama yönteminin , orijinal mesajın hatasız ve kusursuz bir şekilde hatasız olarak algılanabilmesi adına benzersiz ve açık bir şekilde çözünebilen bir kod oluşturulması gereği oldukça açıktır.
En yüksek olasılıkla üretilen mesaj diğer mesajlardan daha fazla sayıda üretilecektir.Böyle bir durumda sabit uzunlukta bir kod yerine değişken uzunlukta bir kod kullanırsanız , düşük olasılıklı mesajlardan daha yüksek olasılıklı mesajlara daha az bit atayarak verimliliği artırabilirsiniz.
MATLAB Programı Nasıl Çalışır ?
Kaynak olasılıklarını azalan sıra ile sıralayın
En düşük olasılıklara sahip iki sembolün olasılıklarını birleştirin ve ortaya çıkan olasılıkları kaydedin.Bu adıma azaltma adımı denmektedir.Bu prosedür ile iki sıralı olasılıklar kalana kadar tekrarlama işlemi yapılır.
Tam olarak iki dereceli olasılıklardan oluşan son indirgenme olayı ile kodlamayı başlatınız.İlk olasılıkla ilişkili tüm kaynak sembolleri için kod kelimelerinde ilk rakam olarak ‘0’ atayın ve ikinci olasılığa ‘1’ atayın.
Şimdi 3. Adımda yapılan tüm atamaları koruyarak önceki redüksiyon adımında birleştirilen iki olasılık için ikinci basamağa geri dönün ve rakamsal olarak ‘0’ ve ‘1’ rakamını atayınız.
İlk sütuna ulaşılana kadar bu şekilde regresyona devam ediniz.
Entropiyi hesaplayınız.Kodun entropisi , belirli bir modeli çözmek için gereken ortalama bit sayısıdır.
Verimliliği hesaplayınız.Oluşturulan kaynak kodunu değerlendirmek için , verimliliği hesaplamanız gerekmektedir.
Verimlilik = Entropi (H(X)) / Ortalama Kod Sözcüğü Uzunluğu (N)
Ortalama kod sözcüğü uzunluğu demek aslında ; N = ∑ (Pi × Ni)’dir.
Ni , Kod sözcüğünün uzunluğudur ve Pi ise oluşma olasılığıdır.
MATLAB Fonksiyonları :
İlki Huffmanenco’dur.Huffman kodlamasında kullanılır.
Söz dizimi ; comp = huffmanenco (sig ,dict) şeklindedir.
Bu satır ‘dict’ sözlüğünde açıklanan ‘sig’ sinyalini kodlar.Argüman olarak ‘sig’ sayısal bir vektördür.Sayısal hücre dizisi veya alfanümerik hücre dizisi biçiminde olabilir.Eğer ‘sig’ bir hücre dizisi ise bir satır ve sütundan oluşmalıdır.’Dict’ , bir Nx2 hücre dizisidir.
Burada ‘N’ kodlanacak farklı olası sembollerin sayısıdır.İlk ‘dict’ sütunu farklı sembolleri temsil eder ve ikinci sütun , ilgili kod kelimelerini temsil eder.Her kod sözcüğü sayısal bir satır vektörü olarak temsil edilir ve ‘kodlamada’ hiçbir kod sözcüğü , diğer kod kelimelerinin önek’i olamaz.Burada Huffmandict işlevini kullanarak ‘dict’ oluşturabiliriz.
İkincisi ise ; Huffmandeco’dur.Bu işlev Huffman kod çözümünde kullanılır.
Söz dizimi : dsig = huffmandeco (comp ,dict)
Burada kod sözlüğü ‘dict’ kullanarak sayısal Huffman Kod vektörünün derlenmesini çözer.’Dict’ argümanı , bir Nx2 hücre dizisidir.Burada ‘N’ , ‘comp’ olarak kodlanmış orijinal sinyaldeki olası sembollerin sayısıdır.İlk ‘dict’ sütunu , farklı sembolleri temsil eder ve ikinci sütun , ilgili kod sözcüğü sayısal bir satır vektörü olarak temsil edilir.
’Kodlamada’ hiçbir kod kelimesinin diğer kod kelimelerinin ön eki olmasına izin verilmez.Huffmanenco işlevini kullanarak Huffmandict işlevini ve ‘comp’ kullanarak ‘dict’ oluşturabiliriz.’Dict’ ifadesindeki tüm sinyal değerleri sayısal ise , ‘dsig’ bir vektördür.’Dict’ ifadesindeki herhangi bir sinyal değeri alfabetik ise , ‘dsig’ tek boyutlu bir hücre dizisidir.
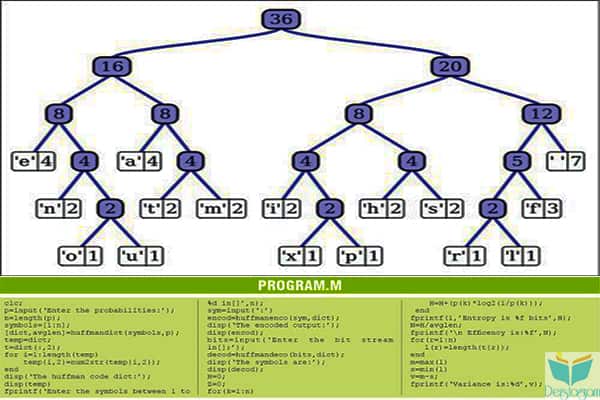
Test Yapalım !
Matlab programını başlatınız.Program ilk olarak mesajların sözlüğünü üretecektir.Bu mesajlar örnekte olduğu gibi 00 ile 1001 arasındaki kodlardan ve bit akışlarından başka bir şey değildir.Kaynak aralığını değiştirerek bu aralığı genişletebilirsiniz.Örnek bir Matlab çıktısı aşağıda verilmiştir;
Olasılıkları giriniz : [0.3 0.25 0.2 0.12 0.08 0.05]
Huffman Kodu Dict ise;
[1] ‘0 0’
[2] ‘0 1’
[3] ‘1 1’
[4] ‘1 0 1’
[5] ‘1 0 0 0 ’
[6] ‘1 0 0 1’
1 ila 6 arasındaki sembollerden birini giriniz :
Örnek olarak []:[3] olsun.
Sym = 3 olduğu için kodlanmış çıkış = 1 1 olacaktır.
Bit akışını da [1 1 ] olarak giriniz.
Semboller ; 3 & Entropi = 2.360147 bit & Verimlilik = 0.991659 & m = 4 & s=2 ve Varyans =2
İlk olarak , program bizden 1 ila 6 arasındaki sayıyı girmenizi ister.3 rakamını girdiğinizde ekranda ‘1 1’ kodu görünür.Bu kod ‘3’ sayısına karşılık gelen karakterden başka bir şey değildir.Bu nedene de kodlama başarılı bir şekilde yapılacaktır.
Kod çözme işlemi içinde bit akışını girmeliyiz (1 1 ).Oluşturulan çıktı ise ‘3’tür.
3 yerine ‘1’ ila ‘6’ arasında çeşitli kombinasyonları deneyebiliriz.
Program bizlere sözlükte üretilen maksimum uzunluk(m) ve minimum uzunluklar (s) değerlerini üretir.Oluşturulan maksimum uzunluk ‘1111’dir.Yani burada m=4 olacaktır.Minimum uzunluk ise ‘00’dır ki burada da iki bit olduğu için minimum uzunluk 2 olacaktır.
Huffman kodlaması aynı zamanda Minimum varyans kodlaması olarakta adlandırılır.Varyans maksimum uzunluk & minimum uzunluktur.Bu nedenle de bu örnek için varyans ‘2’dir.
KAYNAK KODU İNDİRMEK İÇİN TIKLAYINIZ !
HUFFMAN ENCODING (KODLAMA) ve DECODING (KOD ÇÖZME) PROJESİ SONUÇ :
Bugünki yazımızda huffman encoding ve decoding projesini sizlerle paylaştık.Bu yazı dizisinde Matlab’e dair fikirler ve projelere devam ediyor olacağız.Umarım faydalı olabiliyoruzdur.
İyi Çalışmalar
