DÜĞÜM ANALİZLERİ TEOREMİ NEDİR ?
Düğüm analizleri teoremi nedir ? Düğüm analizleri teoremi ile mesh(ağ) analizleri yöntemi arasındaki fark nedir ? Düğüm analizleri yöntemi nerelerde ve nasıl kullanılır ? Bu ve benzeri sorulara yanıt aradığımız Düğüm Analizleri Yöntemi Nedir adlı yazımızla karşınızdayız.
Başlayalım.
DÜĞÜM ANALİZLERİ TEOREMİ
Nodal(Düğüm) Gerilim Analizi, önceki mesh(ağ) analizi ile aynı derecede güçlü ve aynı matris analizi kavramlarına dayanmaktadır.
Adından da anlaşılacağı gibi, düğüm gerilim analizi, devre etrafındaki gerilim potansiyellerini bulmak için Kirchhoff’un birinci yasasına dayanan “Düğüm” denklemlerini kullanır.
Böylece tüm bu düğüm gerilimlerini bir araya getirdiğimizde , net sonucun , toplamların sıfıra eşit olacağını söyleyebiliriz.
Daha sonra, eğer devrede “n” düğüm varsa, “n-1” bağımsız düğüm denklemleri olacaktır ve bunlar yalnız devreyi tanımlamak ve dolayısıyla çözmek için yeterlidir.
Her düğüm noktasında Kirchhoff’un ilk kanun denklemini yazınız, yani: “bir düğüme giren akımlar, düğümü terk eden akımlara tam olarak eşittir”, ardından daldaki voltaj cinsinden her akımı ifade eder.
“N” düğümleri için bir düğüm referans düğümü olarak kullanılacak ve diğer tüm gerilimler bu ortak düğüme göre referanslanacak veya ölçülecektir.
Örneğin, önceki yazılarımızda paylaşılan devreyi düşünün.
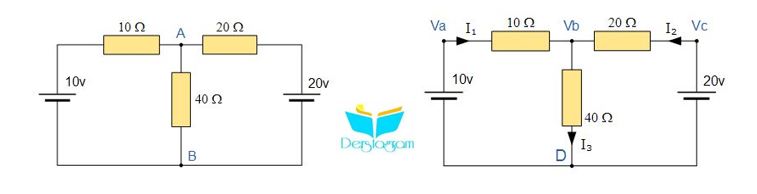
Ağ Gerilim Analiz Devresi
Resimdeki devrede, D düğümü referans düğümü olarak seçilir ve diğer üç düğümün D düğümü ile ilgili olarak Va, Vb ve Vc gerilimlerine sahip olduğu varsayılır. Örneğin;
(Va – Vb) / 10 + (Vc – Vb) / 20 = Vb/40
Va = 10v ve Vc = 20v olduğundan, Vb kolayca bulunabilir:
(1 – (Vb/10)) + (1- (Vb/20)) = Vb/40
2 = Vb x ((1/40) + (1/20) + (1/10))
Vb = (80/7) x V
I3 = (2/7) ya da 0.286 amper
Yine 0.286 amper aynı değeri, bir önceki yazımızda Kirchhoff’un Devre Yasasını da kullanarak bulmuştuk.
Hem Mesh hem de Nodal Analiz yöntemlerini inceledik, ki burada belirli devreyi çözmenin en basit yöntemi budur.
Genel olarak, etrafta daha fazla sayıda akım kaynağı olduğunda, düğüm voltaj analizi daha uygundur. Şebeke daha sonra şöyle tanımlanır:
[I] = [Y] x [V] akım kaynaklarıdır, [V] bulunacak düğüm gerilimleridir ve [Y] ise [V]’a [I] vermek için çalışan ağın matrisidir.
Düğüm Gerilim Analizi Özeti;
Nodal Analiz denklemlerinin çözümü için temel prosedür aşağıdaki gibidir:
1.Akımların bir düğüm içerisindeki pozitif olduğunu varsayarak mevcut vektörleri yazın.Yani, “N” bağımsız düğümler için bir (N x 1) matris.
2. Ağın matrisini [Y] yazınız:
Y11 = ilk düğümün toplamı
Y22 = ikinci düğümün toplamı
RJK = J düğümüne ve K düğümüne katılan toplam
3. “N” bağımsız düğümleri olan bir ağ için, [Y] bir (N x N) matris olacak ve Ynn pozitif ve Yjk negatif veya sıfır değerinde olacaktır.
4. Gerilim vektörü (N x L) olacak ve bulunacak “N” gerilimlerini listeleyecektir.
Şimdi lineer devrelerin analizini basitleştiren bazı teoremlerin var olduğunu gördük.Bir sonraki derste, doğrusal dirençler ve kaynaklardan oluşan bir ağın, tek bir voltaj kaynağı ve bir seri direnç ile eşdeğer bir devre ile temsil edilmesini sağlayan Thevenin Teoremine bakacağız.
DÜĞÜM ANALİZLERİ TEOREMİ SONUÇ :
Bugün Düğüm Analizleri Teoremi adlı yazımızı sizlerle paylaştık.Umuyorum faydalı birtakım bilgiler edinmişsinizdir.
İyi Çalışmalar
