BİNARY DESİMAL RAKAM DÖNÜŞÜMLERİ
Binary rakamlar nedir ? Desimal rakamlar nedir ? Binary rakamlar desimale ve desimal rakamlar binary rakamlara nasıl dönüştürülür ? Bu ve benzeri sorulara yanıt aradığımız Binary Desimal Rakam Dönüşümleri adlı yazımızla karşınızdayız.
Başlayalım.
BİNARY DESİMAL DÖNÜŞÜMLERİ
İkili değerin ondalık sayıya (taban-2 ila taban-10) sayı ve geri dönüşümü, ikili sayı sisteminin tüm bilgisayar ve dijital sistemler için temel oluşturduğundan anlaşılması gereken önemli bir kavramdır.
Ondalık ya da “binary” sayma sistemi, bir sayıdaki her basamağın 0 ile 9 arasındaki “basamak” olarak adlandırılan on olası değerden birini aldığı 10 taban numaralandırma sistemini kullanır.
21310 (İki Yüz ve On Üç)
Ancak, 10 rakamı (0 – 9) içermesinin yanı sıra, ondalık numaralandırma sistemi ayrıca toplama (+), çıkarma (-), çarpma (×) ve bölme (÷) işlemlerine de sahiptir.
Ondalık bir sistemde her hane bir önceki sayıdan on kat daha büyük bir değere sahiptir ve bu ondalık sayı sistemi bir sayıdaki her basamağın ağırlığını belirlemek için bir tabanla(q) birlikte bir sembol seti (b) kullanır.
Örneğin, altmıştaki altı ,altı yüzdeki altıdan daha düşük bir ağırlığa sahiptir.
Bir ikili numaralandırma sisteminde, Ondalıktan İkili’ye ve ayrıca İkiliden Ondalık’a dönüştürmenin bir methodu vardır.
Herhangi bir numaralandırma sistemi aşağıdaki ilişkiyle özetlenebilir:
N = biqi
Burada ;
N = Real pozitif sayıdır
B = rakamdır
Q = taban değeridir
Ve integer olan ‘i’ değeri pozitif , negatif ya da ‘0’ olabilir.
N = bnqn……..b3q3+b2q2+b1q1+b0q0+b-1q-1… gibi
Ondalık Numaralama Sistemi
Ondalık, taban 10’dan veya binary numaralandırma sisteminde, her bir tam sayı sütunu, sayıyı sağdan sola doğru hareket ettirirken birim değer, onlar, yüzler, binler vs. değerlerine sahiptir.
Matematiksel olarak bu değerler 100, 101, 102, 103 vb. olarak yazılır.Ve ondalık basamağın solundaki her konum, 10’luk artı bir artı gücü ifade eder.
Aynı şekilde, kesirli sayılar için sayı, hareket ettikçe daha negatif hale gelir. soldan sağa, 10-1, 10-2, 10-3 vb.
Böylece “ondalık sayı sisteminin” bu sayı sistemindeki her basamağının q ile 10’a (0-9 arası) eşittir olduğunu belirten ve ondalık basamağın içindeki her basamağın bulunduğu 10 ya da 10 tabanına sahip olduğunu görebiliriz.
Örneğin, 20 (yirmi), 2 x 101 demekle aynıdır ve aynı şekilde 400 (dört yüz), 4 x 102 demekle aynıdır.
Herhangi bir ondalık sayının değeri, kendi değerleri ile çarpılan rakamlarının toplamına eşittir. Örneğin: N = 616310 (Altı Bin Yüz Yüz Altmış Üç) ondalık biçimde ;
6000 + 100 + 60 + 3 = 6163
veya her basamağın değerini yansıtacak şekilde yazılabilir:
(6 x 1000) + (1 x 100) + (6 x 10) + (3 x 1) = 6163
veya polinom biçiminde şöyle yazılabilir:
(6 x 103) + (1 x 102) + (6 x 101) + (3 x 100) = 6163
Bu ondalık sayı sistemi örneğinde, en soldaki hane en anlamlı hane veya MSD’dir ve en sağdaki hane en az önemli hane veya LSD’dir.
Başka bir deyişle, en fazla konumu en fazla ağırlığı taşıdığı için 6 rakamı MSD’dir ve en fazla konumu en az ağırlığı taşıdığı için 3 sayısı LSD’dir.
İkili Numaralandırma Sistemi
İkili Numaralandırma Sistemi, tüm dijital ve bilgisayar tabanlı sistemlerdeki en temel numaralandırma sistemidir ve ikili sayılar, ondalık sayı sistemi ile aynı kurallara uyar.
Ancak, onluk güç kullanan ondalık sistemin aksine, ikili sayı sistemi, taban-2’den taban-10’a ondalık dönüştürmeyi sağlayan ikilikn güçlerin üzerinde çalışır.
Dijital mantık ve bilgisayar sistemleri, bir koşulu, “1” mantık seviyesini veya “0” mantık seviyesini temsil etmek için sadece iki değer veya durum kullanır ve her “0” ve “1” temelde 2 tabanlı Binary numaralandırma sistemi şeklinde tek bir rakam olarak kabul edilir.
İkili numaralandırma sisteminde, 101100101 gibi bir ikili sayı, dizi boyunca her bir rakam sağdan sola, bir önceki hanenin iki katı değere sahip olacak şekilde “1” ve “0” dizeleriyle ifade edilir.
Ancak ikili bir rakam olduğundan, yalnızca “1” veya “0” değerine sahip olabilir, bu nedenle q, dizideki kuvveti gösteren konumu 2’ye yani 0 veya 1’e eşittir.
Ondalık sayı, onluktan ikiliye dönüştürme taban10’dan taban2’ye, en sağda en az değerli bit veya LSB ve en solda en çok değerli bit olmak üzere bir ikili sayı üretecektir ve en önemli bit veya MSB olması durumunu şu şekilde temsil edebiliriz:
İkili Sayının Temsili
MSB LSB
| 2^8 | 2^7 | 2^6 | 2^5 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 |
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Yukarıda, ondalık sayı sisteminde, her basamağın sağdan sola kuvvetinin 10 kat arttığını gördük.İkili sayı sisteminde, her basamağın ağırlığının gösterildiği gibi 2 kat arttığı görüldü.
Sonra birinci hane 1(2^0) kuvvete ve ikinci hane 2(2^1) kuvvete, üçüncü hane 4(2^2) kuvvete, dördüncü 8(2^3) kuvvete ve benzerlerine sahiptir.
Örneğin, bir Binary sayının Ondalık sayıya dönüştürülmesi şöyle olacaktır:
Ondalık Rakam Değeri :256 128 64 32 16 8 4 2 1
İkilik Rakam Değeri : 1 0 1 1 0 0 1 0 1
Tüm desimal rakamları bir araya getirerek, “1” ile gösterilen konumlarda sağdan sola ondalık sayı değerleri bize verir: (256) + (64) + (32) + (4) + (1) = 35710 veya ondalık sayı olarak üç yüz ve elli yedi.
Ardından, 1011001012 rakam dizisinin ondalık eşdeğerini bularak ve ikili rakamları ondalık basamağın veya desimal olarak 35710‘a denk gelen 2 tabanına sahip bir seriye genişleterek ikiliyi ondalık sayıya dönüştürebiliriz.
Sayı dönüşüm sistemlerinde ilgili temel numaralandırma
sistemini belirtmek için indislerin kullanıldığını unutmayın, 10012 = 910.
Bir sayıdan sonra indis kullanılmazsa, genellikle ondalık sayılacağı
varsayılır.
Tekrarlayan 2’ye Bölüm Methodu
Yukarıda ikilik sayıları ondalık sayılara nasıl dönüştüreceğimizi gördük, ancak ondalık sayıyı ikili sayıya nasıl dönüştürebiliriz.Ondalık sayıyı ikili sayı eşdeğerlerine dönüştürmenin kolay bir yöntemi, ondalık sayıyı yazmak ve sonuç açısından kalan 0’a eşit olana kadar bir “1” ya da “0” geri kalanını vermek için sürekli sayıyı 2’ye (iki) bölmektir.
Örneğin , 29410 ondalık sayısını ikili sayı eşdeğerine dönüştürün.
294 / 2 = 147 , kalan 0 (LSB)
147 / 2 = 73 , kalan 1
73 / 2 = 36 , kalan 1
36 / 2 = 18 , kalan 0
18 / 2 = 9 , kalan 0
9 / 2 = 4 , kalan 1
4 / 2 = 2 , kalan 0
2 / 2 = 1 , kalan 0
1 / 2 = 0 , kalan 1 (MSB)
Her ondalık basamağın gösterildiği gibi “2” ye bölünmesi sonucu artı kalanı verir.
Eğer bölünen ondalık sayı eşitse, sonuç bütün olacaktır ve geri kalanlar “0” a eşit olacaktır.Ondalık sayı tek ise, sonuç tam olarak bölünmeyecek ve geri kalan kısım “1” olacaktır.
İkili sonuç, en az anlamlı bit (LSB) en üstte ve en önemli bit (MSB) en altta olacak şekilde sırayla bütün kalanlar yerleştirilerek elde edilir.
Bu durumda 29410 ondalık basamağını sağdan sola okuyarak, ikili sayıdaki 1001001102‘e eşdeğerdir. Bu 2’ye bölme yöntemi aynı zamanda diğer sayı tabanlarına dönüştürme için de çalışacaktır.
Sonra bir İkili Numaralandırma Sisteminin temel özelliklerinin, her bir “ikili basamağın” veya “bit” in “1” veya “0” değerinde olduğunu ve her bitin bir önceki bitin iki katı kuvvetinde veya değerinde olduğunu görüyoruz ve burada en düşük veya en az anlamlı bitten (LSB) başlayarak buna “ağırlıkların toplamı” yöntemi denir.
Böylece bir ondalık sayıyı, ağırlık toplamı yöntemini kullanarak ya da tekrarlanan 2’ye bölünme yöntemini kullanarak ikili sayıya dönüştürebiliriz ve ikili değeri ağırlık toplamını bularak ondalık sayıya dönüştürebiliriz.
İkili Sayı İsimleri ve Önekler
İkili sayılar bir araya getirilebilir ve tıpkı ondalık sayılar gibi çıkarılabilir, sonuçta kullanılan bit sayısına bağlı olarak birkaç boyut aralığından birine birleştirilir.
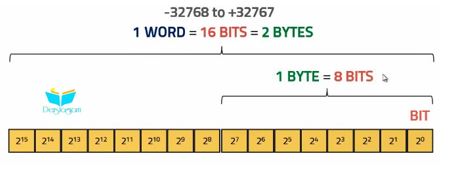
İkili sayılar üç temel biçimde gelir: Bit , Byte ve Word.
Burada bir bit tek Binary rakamı olarak geçer ve bir byte ise 8 binary rakamı ya da 8 bit’e eşittir ve bir Word ise 16 binary rakamı ya da 16-bit’e eşittir.Binary rakam derken 0 ya da 1 manasındadır ve aslında bu durumda da 0 ya da 1 , bir bit demektir.
Bireysel bitlerin daha büyük gruplar halinde sınıflandırılması genellikle aşağıdaki daha genel isimlerle belirtilir:
| Bitlerin Sayısı | Genel İsimlendirme |
| 1 | Bit |
| 4 | Nibble |
| 8 | Byte |
| 16 | Word |
| 32 | Double Word |
| 64 | Quad Word |
Ayrıca, İkilikten Ondalığa ya da Ondalıktan İkiliğe bile dönüştürürken, iki sayı kümesini karıştırmamaya dikkat etmemiz gerekir.Örneğin, 10 rakamını bir sayfaya yazarsak bu desimal tabanda 10 anlamına gelebilir veya bu ikilik tabanda 1 ve 0 olarak yanyana gelmiş Binary sistemdeki bir rakam olabilir ki burada asıl anlatılmak istenen rakamların tabanlarının önemidir.
İkilik sayıyı ondalık sayıya dönüştürürken bu sorunun üstesinden gelmenin ve kullanılan basamakların ya da sayıların ondalık ya da ikili olup olmadıklarını saptamanın bir yolu, son sayıdan sonra sayı sisteminin tabanını göstermek için “alt simge” olarak adlandırılan küçük bir sayı yazmaktır.
Örneğin, eğer bir ikili sayı dizisi kullanıyor olsaydık, bir 2 tabanı sayısını belirtmek için “2” alt ekini eklerdik, böylece sayı 102 olarak yazılırdı.Aynı şekilde, eğer standart bir ondalık sayı olsaydı, alt diziyi eklerdik.“10” tabanlı olan bir sayıda 10 sayısını gösterir, böylece sayı 1010 olarak yazılır.
| Byte Sayısı | Genel İsim |
| 1024 (2^10) | Kilobyte (kb) |
| 1048576(2^20) | Megabyte(Mb) |
| 1073741824 (2^30) | Gigabyte(Gb) |
| 1099511627776 (2^40) | Terabyte (Tb) |
Binary’den Desimal’e Dönüşüm Özeti
“Bit”, BInary digiT‘den türetilmiş kısaltılmış terimdir.
İkili bir sistemde sadece iki durum vardır; Mantık “0” ve Mantık “1” 2 tabanını verir.
Ondalık bir sistem 10 farklı basamak kullanır, 10 tabanında 0 – 9 arası rakamlar
İkili sayı, kuvvet değeri sağdan sola artan bir sayıdır.
İkili bir basamağın kuvveti sağdan sola doğru ikiye katlanır.
Ondalık bir sayı, ağırlıkların toplamı yöntemi veya tekrarlanan 2’ye bölünme yöntemi kullanılarak ikili sayıya dönüştürülebilir.
Sayıları ikili tabandan ondalıklıya veya ondalıklıdan ikiliye dönüştürdüğümüzde, hataları önlemek için indisler kullanılır.
İkilik sistemden ondalık sayıya dönüştürülmesi (2’lik tabandan 10’luk tabana) ya da ondalık sayının (10’luk tabandan 2’lik tabana), yukarıda gösterildiği gibi farklı şekillerde gerçekleştirilmesi mümkündür.
Ondalık sayıları ikili sayılara dönüştürürken, hangisinin en az anlamlı bit (LSB) ve hangisinin en çok anlamlı bit (MSB) olduğunu hatırlamak önemlidir.
BİNARY DESİMAL RAKAM DÖNÜŞÜMLERİ SONUÇ:
Bugün Binary Desimal Rakam Dönüşümleri adlı yazımızı sizlerle paylaştık.Umuyorum faydalı birtakım bilgiler edinmişsinizdir.
İyi Çalışmalar
