MESH(AĞ) AKIM ANALİZİ NEDİR ?

Mesh (Ağ) akım analizi nedir ? Mesh akım analizi nerelerde kullanılır ? Mesh akım analizinin çalışma prensibi nedir ? Bu ve benzeri sorulara yanıt aradığımız Mesh(Ağ) Akım Analizi Nedir adlı yazımızla karşınızdayız.

MESH(AĞ) AKIM ANALİZİ

Kirchhoff Kanunları bize herhangi bir karmaşık elektrik devresini analiz etmek için temel yöntemi verirken, matematiğin azalmasına neden olan ve büyük ağlar söz konusu olduğunda Mesh Akım Analizi veya Nodal Gerilim Analizi kullanarak bu yöntemin iyileştirilmesinin farklı yolları vardır. Ve matematikte bu azalma büyük bir avantaj olabilmektedir.

Mesh(Ağ) Akımı Analiz Devresi

Kullanılan matematiğin miktarını azaltmanın basit bir yöntemi, iki dirençte akan akımları (I1 ve I2) belirlemek için Kirchhoff’un Mevcut Yasa denklemlerini kullanarak devreyi analiz etmektir.

O zaman I3 akımını sadece I1 ve I2 toplamı olarak hesaplamaya gerek yoktur.Böylece Kirchhoff’un ikinci gerilim yasası şöyle olur:

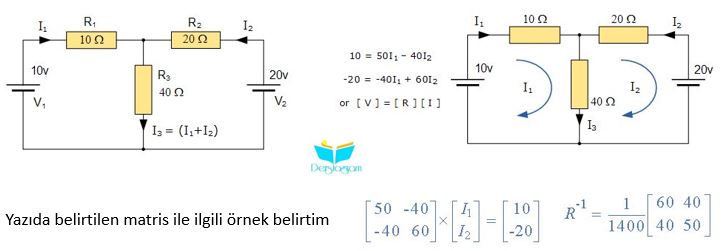
(Bir önceki konuda verilen örnek üzerinden gidilmiştir -> Kirchhoff kanunu yazısı)

Denklem No 1: 10 = 50I1 + 40I2

Denklem No 2: 20 = 40I1 + 60I2 bu nedenle, bir matematik hesaplama satırı kurtarılmıştır.

Mesh (Ağ) Akımı Analizi

Yukarıdaki devreyi çözmenin daha kolay bir yöntemi, bazen Maxwell’in Dolaşan Akımları yöntemi olarak da adlandırılan Mesh Akımı Analizi veya Döngü Analizi kullanmaktır.Dal akımlarını etiketlemek yerine, her “kapalı döngüyü” dolaşan bir akımla etiketlememiz gerekir.

Genel bir kural olarak, devrenin tüm elemanlarını en az bir kere kaplamak olduğundan, döngü içindeki dolaşım akımları olan saat yönünde yalnızca etiketin içindeki etiketi işaretleyin.

Gerekli herhangi bir dal akımı, Kirchhoff metodu kullanılmadan önce uygun loop veya ağ akımlarından bulunabilir.

Örneğin: i1 = I1, i2 = -I2 ve I3 = I1 – I2

Şimdi Kirchhoff’un voltaj yasası denklemini daha önce çözdüğümüz gibi yazıyoruz ancak bu yöntemin avantajı, devre denklemlerinden elde edilen bilginin devreyi çözmek için gereken minimum bilgi olmasını sağlamaktır. Kolayca matris formuna alınabilir.

Örneğin, önceki bölümdeki devreyi düşünün.

Bu denklemler, tek bir ağ empedans matrisi Z ,kullanılarak oldukça hızlı bir şekilde çözülebilir.Ana köşegen üzerindeki her eleman “pozitif” olacaktır ve her bir ağın toplam empedansıdır.

Asıl diyagonal kapalı olan her eleman “sıfır” ya da “negatif” olduğunda, tüm uygun ağları birleştiren devre elemanını temsil eder.

İlk önce, matrislerle uğraşırken, iki matrisin bölünmesi için, bir matrisin gösterildiği gibi diğerinin tersiyle çarpılması ile aynı olduğunu anlamamız gerekir.

Burada , matris olarak 2×2 matris , soldan sağa ilk satır 50 , -40 ve ikinci satır -40,60  x diğer matris 1×2’dir ilk satır I1 ve ikinci satır I2’dir.Sonuç ilk satır 10 ve ikinci satır -20’dir.

Burada I = V/R olduğundan -> ( R^-1 ) x V

R’nin tersi ise matris 2×2 -> ilk satır 60 40 , ikinci satır 40 50

|R| = (60×50) – (40×40) = 1400 olur

R^-1 ise = (1/1400) x matris ilk satır 60 40 , ikinci satır 40 50 olacaktır.

R‘nin tersini bulduktan sonra, V R, VxR^-1 ile aynı olduğundan, şimdi onu iki dolaşım akımını bulmak için kullanabiliriz.

I = R^-1 x V

Matris ilk satır I1 ve ikinci satır I2 = (1/1400) x [matris ilk satır 60 40 , ikinci satır alt 40 50] x [matris ilk satır 10 ikinci alt satır -20]

I1 = ((60 x 10) + (40x-20))  / 1400 = -200 / 1400 = – 0.143 A

I2 = ((40×10) + (50x-20)) / 1400 = -600 / 1400 = -0.429

Burada

[V] loop 1 ve ardından loop 2 için toplam batarya voltajını verir

[I] bulmaya çalıştığımız döngü akımlarının adlarını belirtir

[R] direnç matrisi

[R^-1], [R] matrisinin tersidir

ve bu, I1’i -0.143 Amper ve I2’yi -0.429 Amper olarak verir.

Ardından: I3 = I1 – I2

Dolayısıyla, I3’ün birleşik akımı şöyle verilmiştir: -0.143 – (-0.429) = 0.286 Amper

0.286 amper aynı değerde, önceki eğitimde Kirchoff devre yasasını kullanarak bulduk.

Mesh(Ağ) Akımı Analizi Özeti

Bu “bak-gör” devre analizi yöntemi, Mesh Akım Analizi denklemlerinin çözümü için temel prosedürle birlikte tüm devre analizi yöntemlerinin en iyisidir:

1. Tüm iç döngüleri dolaşımlı akımlarla etiketleyin. (I1, I2,… IL vb.)

2. Her döngüdeki tüm voltaj kaynaklarının toplamını vererek [L x 1] sütun matrisini [V] yazın.

3. Devredeki tüm dirençler için [L x L] matrisini [R] aşağıdaki gibi yazın:

  R11 = ilk döngüdeki toplam direnç.

  Rnn = Nth döngüdeki toplam direnç.

  RJK = doğrudan döngü J’ye Loop K ile bağlanan direnç

4. Matris veya vektör denklemini yazın [V] = [R] x [I], burada [I] bulunacak akımların listesidir.

Mesh Akım Analizi’ni kullanmanın yanı sıra, döngülerin etrafındaki voltajları hesaplamak için düğüm analizini kullanabiliriz, yine sadece Kirchoff yasalarını kullanarak gereken matematik miktarını azaltabiliriz. DC devre teorisi ile ilgili bir sonraki derste, bunun için Nodal Gerilim Analizine bakacağız.

MESH(AĞ) AKIM ANALİZİ SONUÇ :

Bugün Mesh(Ağ) Akım Analizi Nedir adlı yazımızı sizlerle paylaştık.Umuyorum faydalı bir yazı olmuştur sizler adına.

İyi Çalışmalar