İNDÜKTİF REAKTANS NEDİR ?

İndüktif reaktans nedir ? Empedans üçgeni ve güç üçgeni nedir ? İndüktif reaktans formülleri nedir ? İndüktif reaktans nerelerde nasıl kullanılır ? Bu ve benzeri sorulara yanıt aradığımız İndüktif Reaktans Nedir adlı yazımızla karşınızdayız.

Başlayalım.

İNDÜKTİF REAKTANS

Şimdiye kadar DC beslemelerine bağlı indüktörlerin davranışlarına baktık ve şimdi bir DC voltajı bir indüktöre uygulandığında, içinden geçen akımın büyümesinin anlık olmadığını ancak indükleyiciler veya geri emf değeri tarafından belirlediğini biliyoruz.

Ayrıca indüktör akımının, 5x zaman sabiti değerinden sonra maksimum sürekli durumuna erişene kadar yükselmeye devam ettiğini gördük.

İndüktif bir bobin içinden akan maksimum akım, yalnızca Ohm değerlikli bobinlerin sargılarının dirençli kısmı ile sınırlıdır ve Ohm yasasından da bildiğimiz gibi, bu akımın V/R formülü ile üzerindeki gerilim oranıyla belirlenir.

Bir indüktör boyunca bir AC voltajı uygulandığında, içinden geçen akımın akışı, uygulanan bir DC voltajınınkinden çok farklı davranır.

Sinüzoidal bir beslemenin etkisi, voltaj ve akım dalga formları arasında faz farkı yaratır.

Şimdi bir AC devresinde, bobin sargılarından geçen akımın karşıtlığı sadece bobinin indüktansına değil, aynı zamanda AC dalga formunun frekansına da bağlıdır.

Bir AC devresindeki bir bobin boyunca akan akıma olan karşıtlık, daha yaygın olarak, devrenin Empedansı (Z) olarak bilinen AC direnci ile belirlenir.

Ancak direnç, DC direncini AC direncinden ayırt etmek için her zaman DC devreleri ile ilişkilidir ve burada ‘Reaktif’ terimi genellikle kullanılır.

Tıpkı direnç gibi, reaktansın değeri de Ohm olarak ölçülür, ancak bunu tamamen dirençli bir değerden ayırt etmesi için X sembolü (büyük harf “X”) kullanılır.

İlgilendiğimiz bileşen bir indüktör olduğundan, bir indüktansın reaktansı “İndüktif Reaksiyon” olarak adlandırılır.

Başka bir deyişle, bir AC devresinde kullanıldığında bir indüktöre elektriksel direnç olarak İndüktif Reaktif olarak adlandırılır.

X_L sembolü verilen İndüktif Reaktans, akımdaki değişime karşı çıkan bir AC devresindeki özelliktir. AC Devrelerdeki Kondansatörler hakkındaki eğitimlerimizde, tamamen kapasitif bir devrede mevcut I_C‘nin gerilimi 90^o ileri olduğunu gördük.

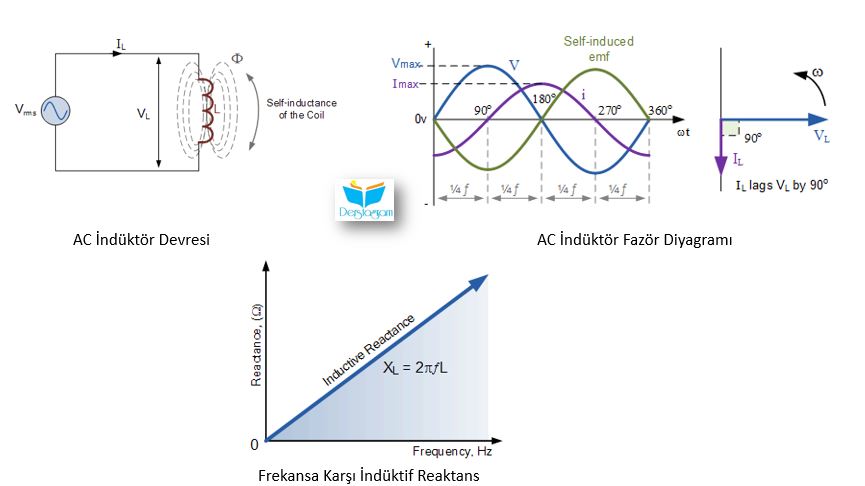
Tamamen ters indüktif bir AC devresinde, bunun tam tersi doğrudur, mevcut I_L, uygulanan gerilimi 90^o (π/2 rad) geridir.

AC İndüktör Devresi

Resimde görebileceğiniz tamamen endüktif devrede, indüktör doğrudan AC besleme voltajına bağlanır.

Besleme gerilimi frekansla birlikte arttıkça ve azaldıkça, kendiliğinden indüklenen geri emf’de bu değişime bağlı olarak bobinde artar ve azalır.

Kendinden kaynaklı bu emf’in, bobinden geçen akımın değişim oranıyla doğrudan orantılı olduğunu ve besleme voltajının pozitif yarı döngüsünden negatif yarı döngüsüne veya tam tersi yönde tersine ve sinüs dalgası boyunca 0° ve 180° boyunca geçtiği için en yüksek değerde olduğunu biliyoruz.

Sonuç olarak, gerilimin minimum değişim hızı, AC sinüs dalgası maksimum veya minimum tepe voltajı seviyesinde geçtiğinde meydana gelir.

Döngüdeki bu pozisyonlarda, maksimum veya minimum akımlar indüktör devresinden akar ve bu resimde gösterilmiştir.

AC İndüktör Fazör Şeması

Bu voltaj ve akım dalga formları, tamamen endüktif bir devre için akımın gerilimi 90o aldığını göstermektedir. Aynı şekilde, voltajın akımı 90o’ya çıkardığını da söyleyebiliriz. Her iki durumda da genel ifade, akımın vektör diyagramında gösterildiği gibi kalmasıdır.

Burada akım vektörü ve voltaj vektörü 90° ile değiştirilmiş olarak gösterilmiştir.

Akım gerilimi keser.

Bu ifadeyi V_L voltajına göre V_L = 0^o ve IL = -90^o olarak da yazabiliriz.

Voltaj dalga formu sinüs dalgası olarak sınıflandırılırsa akım, I_L negatif kosinüs olarak sınıflandırılabilir ve akımın değerini herhangi bir zamanda şu şekilde tanımlayabiliriz:

I_L = Imax x sin(wt-90°) 

Burada: ω saniye başına radyan cinsinden ve t saniye cinsindendir.

Akım, voltajı tamamen endüktif olan bir devrede daima 90^o azalttığından, voltajın fazını bilerek akımın fazını bulabiliriz veya bunun tersini de yapabiliriz.

Öyleyse eğer V_L‘nin değerini biliyorsak, I_L 90^o geride olacaktır diyebiliriz.

Aynı şekilde, eğer I_L‘nin değerini biliyorsak, V_L‘nin 90^o‘ye kadar çıkması gerekir.

Daha sonra endüktif bir devrede bu akıma gerilim oranı, bobinin X_L Endüktif Reaktifini tanımlayan bir denklem üretecektir.

Endüktif reaktans

X_L = V_L/I_L = wL(Ω)

İndüktif reaktans için yukarıdaki denklemi radyan açısal frekans yerine arzın normal frekansını kullanan daha bilinen bir formda yeniden yazabiliriz, ve ω ile bu şöyle verilir:

X_L = 2 x π x f x L  

Burada: ƒ Frekans ve L, Bobinin İndüktansıdır ve 2πƒ = ω’dur.

İndüktif reaktans için yukarıdaki denklemden, Frekans veya İndüktansın arttırılması durumunda, toplam endüktif reaktans değerinin de artacağı görülebilir.

Frekans sonsuzluğa yaklaştığında indüktörler reaktansı açık devre gibi davranarak sonsuzluğu artacaktır.

Bununla birlikte, frekans sıfıra veya DC’ye yaklaştığından, indüktörlerin reaktansı kısa devre gibi davranarak sıfıra düşer.

Bu, endüktif reaktansın frekansla “orantılı” olduğu anlamına gelir.

Başka bir deyişle, endüktif reaktans, düşük frekanslarda X_L‘nin küçük ve yüksek frekanslarda X_L‘nin yüksek olmasıyla sonuçlanan frekansla artar ve bu, resimdeki grafikte gösterilmiştir:

Frekansa Karşı Endüktif Reaksiyon

Eğim, bir endüktansın “Endüktif Tepkimesinin”, karşısındaki besleme frekansı arttıkça arttığını gösterir.

Bu nedenle Endüktif Reaktans, frekans ile orantılıdır: (X_L α ƒ)

Daha sonra DC’de bir indüktörün sıfır reaktansa (kısa devre), yüksek frekanslarda bir indüktansın sonsuz reaktansa (açık devre) sahip olduğunu görebiliriz.

Endüktif Reaktans Örneği 1:

Bir 150mH indüktans bobini ve sıfır direnç, bir 100V, 50Hz’lik beslemeye bağlanır.

Bobinin indüktif reaktansını ve içinden geçen akımı hesaplayın.

İndüktif reaktans : X_L  = 2 x π x f x L   = 2 x π x 50 x 0.15 = 47.12Ω

Akım : I = V / X_L  = 100 / 47.12 = 2.12A

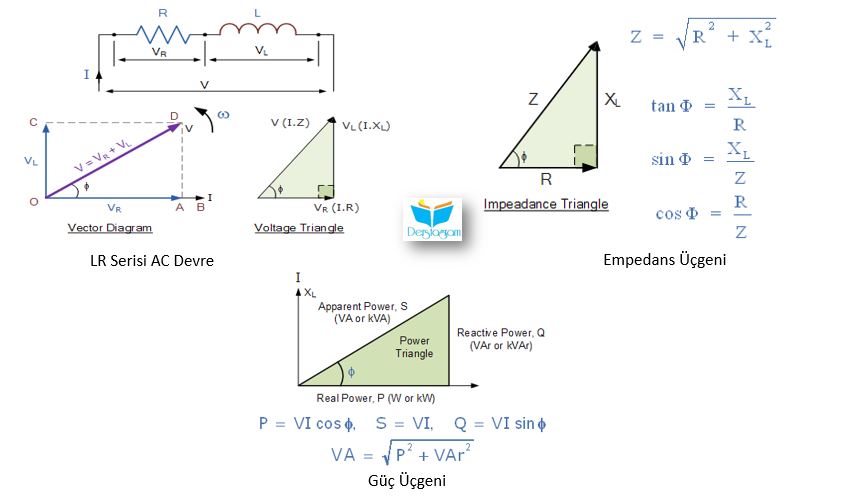
LR Serisi Devre Üzerinden AC Beslemesi

Şimdiye kadar tamamen indüktif bir bobin olarak düşündük, ancak tüm bobinler, röleler veya solenoidler, kullanılan bobinlerin dönüşleri ile ne kadar küçük olursa olsun, belirli bir direnç derecesine sahip olacaklarından, saf bir indüktans olması imkansızdır.

O zaman basit bobini indüktanslı seri halde direnç olarak değerlendirebiliriz.

Hem indüktans, hem L hem de direnç içeren bir AC devresinde R voltajı, V iki bileşen voltajının fazör toplamı olacaktır, V_R ve V_L.

Bu, daha sonra, bobinden geçen akımın hala voltajı düşüreceği, ancak V_R ve V_L değerlerine bağlı olarak 90^o‘den daha az bir miktarda olacağı anlamına gelir.

Gerilim ve akım arasındaki yeni faz açısı, devrenin faz açısı olarak bilinir ve Yunanca sembol phi olarak adlandırılır.

Gerilim ve akım arasındaki ilişkinin bir vektör diyagramını üretebilmek için bir referans veya ortak bileşen bulunmalıdır.

Bir seri bağlı R-L devresinde, akım aynı bileşen ve her bileşen boyunca akarken aynıdır.

Bu referans miktarının vektörü genellikle soldan sağa yatay olarak çizilir.

Dirençler ve kapasitörler hakkındaki eğitimlerimizden, dirençli bir AC devresindeki akım ve voltajın hem “faz içi” hem de vektör olduğunu biliyoruz, bu nedenle V_R, akım veya referans çizgisine ölçeklendirmek için üst üste çizilir.

Ayrıca yukarıdan biliyoruz ki, akımın tamamen indüktif bir devrede gerilimini “düşürdüğü” ve bu nedenle vektör, V_L akım referansının önüne ve V_R ile aynı skalaya çekilir ve bu resimde  gösterilmiştir.

LR Serisi AC Devresi

Resimdeki vektör diyagramında, OB hattının mevcut referans hattını temsil ettiği, OA hattının dirençli bileşenin voltajı olduğu ve akımla aynı fazda olduğu görülebilir.

OC hattı, akımın önünde 90^o olan indüktif voltajı gösterir, bu nedenle akımın voltajı 90^o kadar düştüğü görülebilir.

OD hattı bize devre boyunca ortaya çıkan ya da besleme gerilimini verir.

Gerilim üçgeni Pisagor teoreminden türetilmiştir ve şöyle verilir:

V² = V_R² + V_L²

V = √V_R²+V_L²

Ve tanɸ = V_L / V_R

Bu sebeple ; V_R = I x R ve V_L = I x X_L

 V = √(I x R)² + (I x XL)²

I = V / √(R²+X_L²) = V/Z (A)

Bir DC devresinde, gerilimin akıma oranına direnç denir.

Bununla birlikte, bir AC devresinde bu oran Empedans olarak bilinir.Empedans, hem direnci hem de indüktif reaktansı içeren bir “AC devresindeki” akım akışına karşı toplam dirençtir.

Voltaj üçgeninin yanlarını akımla bölersek, yanları bobinin direnci, reaktansı ve empedansını temsil eden başka bir üçgen elde edilir.

Bu yeni üçgene “Empedans Üçgeni” denir. Resimde görebilirsiniz.

Endüktif Reaksiyon Örneği 2:

Bir solenoid bobin 30 Ohm’luk bir dirence ve 0.5H’lik bir indüktansa sahiptir.

Bobinden akan akım 4 amper ise,

a) Frekans 50Hz ise, besleme voltajı nedir ?

X_L = 2 x π x f x L  = X_L = 2 x π x 50 x 0.5 => 157Ω

Z = √(R²+X_L²) = > √30²+157²  = 160 Ω

V = I x Z  = 4 x 160 = 640V

b) Gerilim ve akım arasındaki faz açısı.

tanɸ = X_L / R => ɸ = (tan ^-1 )x (X_L/R) = 157/30 = 79.2 derecelik bir gecikme

Bir AC İndüktörünün Güç Üçgeni

Endüktif devre için kullanabileceğimiz ve “Güç Üçgeni” olan başka bir üçgen konfigürasyon tipi daha vardır.

Endüktif bir devredeki güç, Reaktif Güç veya volt-amper reaktif, volt-amper olarak ölçülen Var sembolü olarak bilinir.

Bir RL serisi AC devresinde, akım besleme gerilimini Φ^o bir açı ile düşürür.

Tamamen endüktif bir AC devresinde akım, besleme voltajına tam olarak 90^o faz dışı olacaktır.

Bu haliyle, bobin tarafından tüketilen toplam reaktif güç, tüketilen herhangi bir güç, üretilen kendi kendine indüklenen emf gücü tarafından iptal edildiğinden sıfıra eşit olacaktır.

Başka bir deyişle, bir tam çevrimin sonunda saf bir indüktör tarafından tüketilen watt cinsinden net güç, enerji hem tedarikten alındığı hem de ona geri verildiği için sıfırdır.

Bir bobinin Reaktif Gücü (Q) aşağıdaki gibi verilebilir:

I² x XL (bir DC devresindeki I²R’ye benzer).

Daha sonra, bir AC devresindeki bir güç üçgeninin üç tarafı, görünür güç, (S), gerçek güç (P) ve reaktif güç (Q) ile gösterildiği gibi gösterilir.

Güç üçgeni

Gerçek bir indüktör veya bobinin, empedans Z, oluşturmada oluşan sarımların direnci nedeniyle watt cinsinden güç tüketeceğine dikkat edin.

İNDÜKTİF REAKTANS NEDİR SONUÇ :

Bugün İndüktif Reaktans Nedir adlı yazımızla karşınızdaydık.Umuyorum sizler adına faydalı bir yazı olmuştur.

İyi Çalışmalar