FİZİK DERSLERİ – 1 GİRİŞ

Fizikte kullanılan kurallar nelerdir ? Kuvvet , kütle , ivme , ağırlık vb. kavramlar nedir ? Kullandığımız materyallerin alan hacim hesaplamaları nasıl yapılır ? Bu ve benzeri sorulara yanıt aradığımız ve aynı zamanda Elektronik/Otomasyon anlamında giriş yazısı olan Fizik Dersleri -1 adlı yazımızı sizlerle paylaşıyoruz.

Başlayalım.

FİZİK DERSLERİ -1

Terimler ve tanımlar

Kütle (m), bir nesnenin hızlanması gereken muhalefettir (hızdaki değişiklikler).

Ağırlık, kütleçekimsel bir alan tarafından kütleye uygulanan kuvvettir (F). Kütle, ortamdan bağımsız olarak nesnenin kendine özgü bir özelliğidir.

Diğer yandan ağırlık, nesnenin bulunduğu yerçekimi alanının gücüne bağlıdır.

Kütlenin ağırlığı yerçekimine bağlıdır: dış uzayda sıfır ağırlık (bunun üzerine etki edecek yerin olmadığı yerler), Dünyadaki bir miktar ağırlık ve Jüpiter gezegeninde (çok daha güçlü olması nedeniyle) çok daha fazla ağırlıktan söz edilebilir.

Kütle, bir nesnenin hızdaki değişikliklere (ivme) karşı olması nedeniyle, herhangi bir belirli nesne için kuvvet için, kütle ve ivme birbirleriyle doğrudan ilişkilidir:

Formül  -> F = ma

Burada

F = Newton kuvveti (metrik)

m = Kilogram (metrik)

a = Saniyedeki metrekare (metrik) cinsinden hızlanma

Söz konusu kuvvet nesnenin ağırlığı ise, söz konusu ivme (a) nesnenin bulunduğu yerçekimi alanının ivmesi sabitidir.

Dünya üzerinde eğer deniz seviyesi için konuşacak olursak, a_yerçekimi ortalama büyüklüğü saniyede yaklaşık 9.81 metre veya 32.2 feet  saniye karedir.

Dünyanın kütleçekimsel ivmesi sabiti, genellikle daha genel olan a yerine g değişkeni harfiyle denklemlerde temsil edilir.

İvme, zamana göre hız değişim hızından başka bir şey olmadığından, kuvvet/kütle denklemi, birinci türevin hesaplanan gösterimi kullanılarak ifade edilebilir:

F = m x (dv/dt)

Burada,

F = Newton kuvveti

m = Kilogram (metrik) cinsinden kütle

v = Saniyedeki metre (metrik) cinsinden hız

t = Saniye cinsinden süre

Hız, zamana göre konum değişim oranından farklı bir şey olmadığından, kuvvet/kütle denklemi, ikinci türevin hesaplanan ifadesi kullanılarak ifade edilebilir (hızlanma, hızın türevidir, sırayla konumun türevidir)

F = m x (d²x/dt²)

Burada,

F = Newton kuvveti

m = Kilogram (metrik) cinsinden kütle

x = Metre olarak pozisyon (metrik)

t = Saniye cinsinden süre

Herhangi bir madde için kütle yoğunluğu (ρ) kütlenin hacme oranıdır.

Herhangi bir madde için ağırlık yoğunluğu (γ), ağırlığın hacme oranıdır.

Tıpkı ağırlık ve kütle çekim kuvveti ile birbiriyle ilişkili olduğu gibi, ağırlık yoğunluğu ve kütle yoğunluğu da kütleçekimi ile ilişkilidir:

F_ağırlık = mg  (Ağırlık ve Kütle)

γ = ρg  (Ağırlık yoğunluğu ve Kütle yoğunluğu)

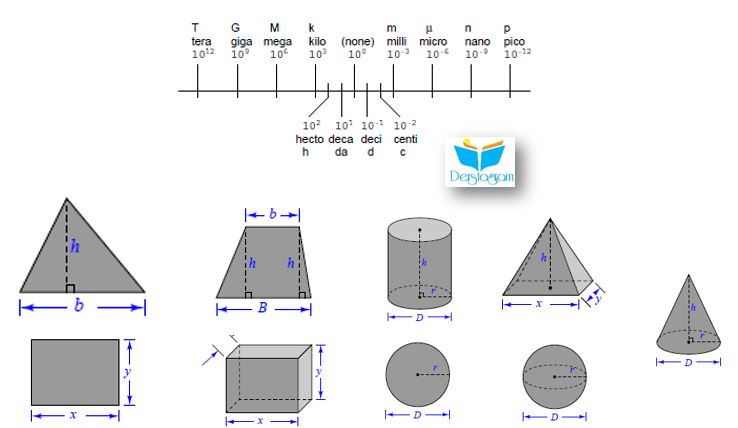
Metrik Önekleri

T : Tera -> 10¹²

G : Giga -> 10⁹

M : Mega -> 10⁶

k : Kilo -> 10³

h : Hecto -> 10²

da : Deca -> 10¹

Ön ek yok , -> 10⁰

d : Deci -> 10^-1

c : Centi -> 10^-2

m : Mili -> 10^-3

m :  Micro ->10^-6

n : Nano ->10^-9

p : Pico -> 10^-12

Alanlar ve Hacimler

Alan, iki boyutlu yüzeyin büyüklüğünü belirtir.Hacim, üç boyutlu bir boşluğun boyutunu ifade eder.

Her ikisini de bir bağlam içine almak adına; Bir evi yeterince kaplamak için ne kadar boya gerektiğine dair soru alanlardan biriyken, bir göleti doldurmak için ne kadar suyun gerekli olacağı sorusu hacim sorusudur.

Alan ve hacim için bazı ölçüm birimleri, bileşik doğrusal birimlerden başka bir şey değildir.

On santimetre, mesafenin bir ifadesiyken, on santimetrekare (cm^2) bir alanın ifadesidir ve on santimetre küp (cm^3) bir hacim ifadesidir.

Örneğin bir santimetrekarelik birimi kullanarak bir dairenin alanını ölçmek tamamen mantıklıdır.

Diğer mekansal ölçüm birimleri, alana veya hacme özgüdür.

Özellikle hacme tahsis edilmiş bir birim örneği olarak litre, 1000 santimetre küptür.

Üçgen Alan : 1/2 x b x h

Yamuk Alan : 1/2 x (b+B) x h

Dikdörtgen Alan : xy , Çevre : 2x+2y

Dikdörtgen Cisim Yüzey Alanı : 2xy + 2xz + 2yz , Hacim (V) : xyz

Çember Çevre : πD = 2πr

Küre Yüzey alanı : 4πr²  , Küre Hacim : 4/3 x π x r³

Doğru Dairesel Silindir Yüzey Alanı ; 2πr² + 2πrh , Hacim : πr²h

Koni Yüzey Alanı : πr√(r²+h²) + πr²  , Hacim : 1/3 πr²h

Tetrahedron (4 Yüzlü Şekil) Hacim : (1/3) x (xyh)

Birim dönüşümler ve fiziksel sabitler

Farklı ölçüm birimleri arasında dönüştürme, birçok kimseler için tanıdık gelecektir.

Sorun, Amerika Birleşik Devletleri’ndeki, İngiliz Sterlini (“Standart”) birimlerinde, pound, foot, galon vb. birimlerle çalışması gereken kimseler için daha kötüdür.

Bu amaç için açıkça tasarlanan tabloları kullanarak bir ölçüm biriminden diğerine dönüştürme mümkündür.

Bu tür tablolar genellikle sol taraftaki birimler sütununa ve üst kısım boyunca aynı birim dizisine sahiptir; bu sayede, listelenen herhangi bir birimden herhangi bir listelenen birime dönüştürmek üzere çarpım için dönüştürme faktörü aranabilir.

Bu tür tabloların kullanımı inkar edilemez derecede basit olsa da, ezberlemek neredeyse imkansızdır.

FİZİK DERSLERİ – 1 GİRİŞ SONUÇ :

Bugün Fizik Dersleri – 1 adlı yazımızı sizlerle paylaştık.Umuyorum faydalı birtakım bilgiler edinmişsinizdir.

İyi Çalışmalar