FAZÖR DİYAGRAMLARI VE CEBİRİ NEDİR ?
Fazör diyagramları nedir ? Dalga formunun fazör şemaları , faz farkı nedir ? Komplex sinüzoidinin tanımı nedir ? 3 fazlı fazör şeması nedir ? Bu ve benzeri sorulara yanıt aradığımız Fazör Diyagramları ve Cebiri Nedir adlı yazımızla karşınızdayız.
Başlayalım.
FAZÖR DİYAGRAMLARI VE CEBİRİ
Fazör Diyagramları, iki veya daha fazla değişken büyüklük arasındaki büyüklük ve yön ilişkisini gösteren grafiksel bir yol , yöntemdir.
Aynı frekanstaki sinüzoidal dalga formları, iki sinüzoidal dalga formunun açısal farkını temsil eden kendi aralarında Faz Farkına sahip olabilir.Ayrıca, “gecikme”, “faz içi” ve “faz dışı” terimleri, bir dalga formunun diğeriyle ilişkisini belirtmek için yaygın olarak kullanılır:
A (t) = Am sin (wt±Φ) ( Zaman alanı formundaki sinüzoidi temsil eder )
Fakat matematiksel olarak bu şekilde sunulduğunda, iki veya daha fazla sinüzoidal dalga formu arasındaki bu açısal veya fazör farkını görselleştirmek bazen zor olabilmektedir.
Bu sorunun üstesinden gelmenin bir yolu, sinüzoidleri Fazör Diyagramları kullanarak uzaysal veya fazör-alan formunda grafiksel olarak temsil edebilirz ve çözüm ise dönen vektör yöntemiyle elde edilebilir.
Temel olarak basitçe “Fazör” olarak adlandırılan dönen bir vektör, uzunluğu belirli bir zamanda “dondurulmuş” olan hem büyüklüğüne (“en yüksek genlik”) hem de yöne (“ faz ”) sahip bir AC miktarını temsil eden ölçekli bir çizgidir.
Bir fazör, bir ucunda bir ok kafasına sahip olan ve vektör miktarının maksimum değerini (V veya I) ve dönen vektörün ucunu gösteren bir vektördür.
Genellikle, vektörlerin bir ucunda, “başlangıç noktası” olarak bilinen sabit bir sıfır noktası etrafında döndüğü varsayılırken, miktarı temsil eden oklu ucun, bir tam devirin açısal hızında (w) her döngü için serbest bir şekilde saat yönünün tersi yönde serbestçe döndüğü durumdur.
Vektörün bu saat yönünün tersine dönmesinin pozitif bir dönme olduğu düşünülmektedir. Aynı şekilde, saat yönünde bir dönüş negatif bir dönüş olarak kabul edilir.
Vektörler ve fazörler terimleri, hem büyüklük hem de yöne sahip dönen bir çizgiyi tanımlamak için kullanılsa da, ikisi arasındaki temel fark, vektörlerin büyüklüğünün sinüzoidin “tepe değeri” iken, bir fazör büyüklüğü “ sinüzoidin rms değeridir”. Her iki durumda da faz açısı ve yönü aynı kalır.
Zamanın herhangi bir anında değişen bir miktarın fazı fazör diyagramı ile gösterilebilir, bu nedenle fazör diyagramları “zamanın fonksiyonu” olarak düşünülebilir.
Tam bir sinüs dalgası ω = 2πƒ açısal hızda dönen tek bir vektör tarafından oluşturulabilir, ki burada ƒ dalga formunun frekansıdır.O zaman bir Fazör, hem “Büyüklük” hem de “Yön” içeren bir miktardır.
Genellikle, bir fazör diyagramı oluşturulurken, bir sinüs dalgasının açısal hızının her zaman olduğu varsayılır : ( w rad/sn )cinsinden.
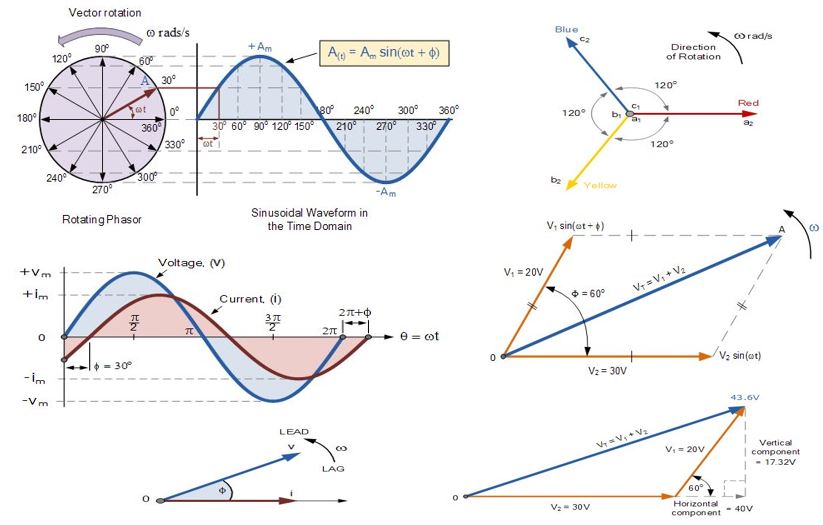
Sinüzoidal Dalga Formunun Fazör Şeması
Tek vektör saat yönünün tersine döndüğü için, A noktasındaki ucu, bir tam çevrimi temsil eden 360 derece veya 2π’lık bir tam devrimi döndürecektir.
Hareketli ucunun uzunluğu, resimde gösterilen bir grafiğe zaman içinde farklı açısal aralıklarla aktarılırsa, soldan başlayarak sıfır zaman ile başlayarak bir sinüzoidal dalga formu çizilecektir. Yatay eksen boyunca her pozisyon, sıfır zamandan beri geçen süreyi, t = 0’ı gösterir.
Vektör yatay olduğunda, vektörün ucu, 0 derece, 180 derece ve 360 derece’deki açıları temsil eder.Benzer şekilde, vektörün ucu dikey olduğunda, pozitif tepe değerini, 90 derece veya π/2’de (+ Am) ve negatif tepe değerini, 270 derece veya 3π/2’de (-Am) temsil eder.
Daha sonra dalga formunun zaman ekseni açıyı fazörün hareket ettiği derece veya radyan cinsinden gösterir.
Bazen, alternatif dalga formlarını analiz ederken, özellikle aynı eksen üzerinde iki farklı dalga formunu karşılaştırmak istediğimizde, Zamanla Değişen Miktarı belirli bir anda temsil eden fazörün konumunu bilmemiz gerekebilir.
Örneğin, voltaj ve akım.
Yine resim üzerindeki dalga biçiminde, dalga biçiminin t = 0 zamanında, derece veya radyan cinsinden karşılık gelen bir faz açısıyla başladığını varsaydık.
Ancak, ikinci bir dalga biçimi bu sıfır noktasının soluna veya sağına başlarsa veya fazör notasyonunda iki dalga biçimi arasındaki ilişkiyi temsil etmek istiyorsak, o zaman dalga biçiminin bu faz farkını dikkate almamız gerekir.
Sinüzoidal Dalga Formunun Faz Farkı
Bu iki sinüzoidal büyüklüğü tanımlayan genelleştirilmiş matematiksel ifade şöyle yazılacaktır:
V(t) = Vm sin (wt)
I(t) = Im sin (wt- Φ)
Akım, i, Φ gecikme açısına göre voltajı geciktirmektedir.Dolayısıyla, iki sinüzoidal miktarı temsil eden iki faz arasındaki fark açı gecikmesi ve sonuçtaki fazör şeması olacaktır.
Sinüzoidal Dalga Formunun Fazör Şeması
Fazör diyagramı, yatay eksende sıfıra (t = 0) karşılık gelecek şekilde çizilir. Fazörlerin uzunlukları, fazör diyagramının çizildiği andaki gerilim, (V) ve akım, (I) değerleriyle orantılıdır.
Akım dalga formu şu anda yatay sıfır eksen çizgisini şu anda geçmekte olduğundan, akım fazörü yeni referansımız olarak kullanabilir ve voltaj fazerin akım fazörü açı ile “yönlendirdiğini” söyleyebiliriz.
Her iki durumda da, bir fazör, referans fazör olarak tanımlanır ve diğer tüm fazörler bu referansa göre öncülük eder veya geciktirilir.
Fazör ilavesi bazen, sinüzoidleri okurken, birbirleriyle aynı fazda olmayan iki alternatif dalga biçimini, örneğin; bir AC serisi devresinde bir araya getirmek gerekir.Eğer faz fazındalarsa, faz kayması olmazsa, iki vektörün cebirsel toplamını bulmak için DC değerleri ile aynı şekilde eklenebilirler.
Örneğin, sırasıyla 50 volt ve 25 volt olan iki voltaj birlikte “faz” ise, 75 volt (50 + 25) bir voltaj oluşturmak için bir arada toplanır.Bununla birlikte, faz-içi değillerse, aynı yönlere veya başlangıç noktalarına sahip değillerdir, o zaman aralarındaki faz açısının dikkate alınması gerekir, bu nedenle Sonuç Fazörleri veya Vektör Toplamını belirlemek için fazör diyagramları ile birlikte eklenmelidirler. (paralelkenar yasasını kullanarak)
İki AC gerilimi, V1’in 20 voltluk bir tepe voltajına sahip olduğu ve V2’nin Vo’yu 60 dereceye getirdiği 30 voltluk bir tepe voltajına sahip olan V2’yi düşünün.
İki voltajın toplam voltajı, VT ilk önce iki vektörü temsil eden bir fazör diyagramı çizilerek ve daha sonra tarafların ikisinin aşağıda gösterildiği gibi V1 ve V2 voltajları olduğu bir paralelkenar oluşturularak bulunabilir.
İki fazörün eklenmesi grafik kağıdına ölçeklenecek iki fazı çizerek, bunların faz toplamları V1 + V2, “sonuçtaki r-vektörü” olarak bilinen çapraz çizginin uzunluğunu sıfır noktasından kesişimine kadar ölçerek kolayca bulunabilir.
Bu grafiksel yöntemin dezavantajı, ölçeklendirmek için fazörleri çizerken zaman alıcı olmasıdır.Ayrıca, bu grafiksel yöntem çoğu amaç için yeterince doğru bir cevap verirken, ölçeklemek için doğru bir şekilde çizilmezse bir hata üretebilir.Her zaman doğru cevabın alınmasını sağlamanın bir yolu analitik bir yöntemdir.
Matematiksel olarak iki gerilimi önce “dikey” ve “yatay” yönlerini bularak birleştirebiliriz ve bundan sonra elde edilen “r vektörü” VT için hem “dikey” hem de “yatay” bileşenleri hesaplayabiliriz.Bu sonuç değerini bulmak için kosinüs ve sinüs kuralını kullanan bu analitik yönteme genellikle Dikdörtgen Form denir.
Dikdörtgen formda, fazör, genelleştirilmiş ifadeyi Z = x ± jy oluşturan, gerçek bir kısma, x ve hayali bir kısma ayrılır.Bu daha sonra bize sinüzoidal voltajın hem büyüklüğünü hem de fazını temsil eden matematiksel bir ifade verir:
Kompleks Sinüzoidin Tanımı
Vm = cos(Φ) + jVm(sin Φ)
Bu nedenle, önceki genelleştirilmiş ifadeyi kullanarak iki vektör, A ve B’nin eklenmesi aşağıdaki gibidir:
A = x + jy
B = w + jz
A+B = (x + w) + j(y+z)
Dikdörtgen Form Kullanarak Fazör Eklemesi
Voltaj, 30 voltluk V2, yatay sıfır ekseni boyunca referans yönünde işaret eder, sonra yatay bir bileşene sahiptir, ancak aşağıdaki gibi dikey bir bileşen yoktur.
- Yatay Bileşen = 30 cos 0 derece = 30 volt
- Dikey Bileşen = 30 sin 0 derece = 0 volt
Bu da bize V2 voltajı için dikdörtgen ifade verir: 30 + j0
Gerilim, 20 voltluk V1, gerilime, 60 dereceye kadar V2’ye neden olur, ardından aşağıdaki yatay ve dikey bileşenlere sahiptir.
- Yatay Komponent = 20 cos 60 derece = 20 x 0.5 = 10 volt
- Dikey Bileşen = 20 sin 60 derece = 20 x 0.866 = 17.32 volt
Bu da bize V1 voltajı için dikdörtgen ifade verir: 10 + j17.32
Elde edilen voltaj, VT, yatay ve dikey bileşenleri aşağıdaki gibi bir araya getirerek bulunur.
Vhorizontal = V1 ve V2’nin gerçek parçalarının toplamı = 30 + 10 = 40 volt
Vvertical = V1 ve V2’nin hayali parçalarının toplamı = 0 + 17.32 = 17.32 volt
Artık hem gerçek hem de hayali değerlerin gerilimin büyüklüğünün bulunduğuna bakıldığında, Vt için basitçe Pythagoras Teoremi kullanılarak, 90 derece üçgen için belirlenir.
VT = √(gerçek ya da yatay komponent)^2 + (hayali ya da dikey komponent)^2
VT = √40^2 + (17.32)^2
VT = 43.6 volt olacaktır.
Fazör Çıkarma
Fazör çıkarma, yukarıdaki dikdörtgen ekleme yöntemine çok benzer, ancak bu sefer vektör farkı, gösterildiği gibi V1 ve V2’nin iki gerilimi arasındaki paralelkenarın diğer köşegendir.
İki Fazörün Vektör Çıkarması
Bu sefer hem yatay hem de dikey bileşenleri bir araya “eklemek” yerine onları uzaklaştırıyoruz, çıkartıyoruz.
A = x + jy
B = w + jz
A – B = ( x – w ) + j(y – z)
3 Fazlı Fazör Şeması
Önceden, sadece tek bir çok turlu bobinin manyetik alan içinde döndüğü tek fazlı AC dalga formlarına baktık.Ancak, her biri aynı sayıda bobin dönüşüne sahip üç özdeş bobin, aynı rotor şaftı üzerinde birbirlerine 120 derece elektrik açısına yerleştirilirse, üç fazlı bir voltaj beslemesi üretilir.
Dengeli bir üç fazlı voltaj beslemesi, hepsi büyüklük ve frekansta eşit olan ancak birbirleriyle tam olarak elektriksel derecelerde 120 faz arasında olan üç ayrı sinüzoidal voltajdan oluşur.
Standart uygulama, her bir fazı referans faz olarak kırmızı faz ile tanımlamak için üç fazı Kırmızı, Sarı ve Mavi olarak renklendirmektir.
Üç fazlı bir besleme için normal dönüş sırası Kırmızı, ardından Sarı, ardından Mavi, (R, Y, B). Yukarıdaki tek fazlı fazlarda olduğu gibi, üç fazlı bir sistemi temsil eden fazörler ayrıca rad/s’de ω ile işaretli okla belirtildiği gibi merkezi bir nokta etrafında saat yönünün tersine yönde döner.
Üç fazlı fazör diyagramı
Faz gerilimlerinin tümü genlikte eşittir, ancak sadece faz açılarında farklılık gösterir. Bobinlerin üç sargısı, üç ayrı faz için ortak bir nötr bağlantı üretmek için, a1, b1 ve c1 noktalarında birbirine bağlanır.
Daha sonra kırmızı faz referans faz olarak alınırsa, her bir ayrı faz voltajı, ortak nötr ile ilgili olarak tanımlanabilir.
Üç Fazlı Gerilim Denklemleri
Kırmızı Faz : Vrn = Vm sin Φ
Sarı Faz : Vyn = Vm sin (Φ – 120 derece)
Mavi Faz : Vbn = Vm sin (Φ – 240 derece) ya da Vbn = Vm sin(Φ +120 derece)
Eğer kırmızı faz voltajı, VRN daha önce belirtildiği gibi referans voltajı olarak alınırsa, faz sırası R – Y – B olacaktır, böylece sarı fazdaki voltaj VRN’yi 120 derece, mavi fazdaki voltaj da VYN’yi 120 derece bırakır.
Ancak mavi faz voltajını şu şekilde söyleyebiliriz, VBN, kırmızı faz voltajını, VRN’yi 120 dereceye kadar yönlendirir.Üç ayrı sinüzoidal voltajın birbirleriyle arasında 120 derece sabit bir ilişki olduğu için, “dengeli” oldukları söylenir, bu nedenle, dengeli bir üç faz gerilimi setinde, fazör toplamı her zaman sıfır olacaktır: Va + Vb + Vc = 0
Fazör Diyagramı Özeti
En basit ifadeleriyle fazör diyagramları, dönen bir vektörün, ani değeri temsil eden yatay bir eksene yansımasıdır.
Herhangi bir zaman anını ve dolayısıyla herhangi bir açıyı temsil etmek üzere bir fazör diyagramı çizilebildiği için, değişken bir nicelikteki referans fazlayıcı daima pozitif x ekseni yönü boyunca çizilir.
Vektörler, Fazörler ve Fazör diyagramları sadece şemalar, sinüzoidal AC alternatif miktarları için geçerlidir.
Herhangi bir anda iki veya daha fazla sabit sinüzoidal miktarı temsil etmek için bir Fazör Diyagramı kullanılabilir.
Genellikle referans fazörü yatay eksen boyunca çizilir ve o sırada diğer fazlar çekilir.
Tüm fazörler yatay sıfır eksenine referansla çizilir.
Fazör diyagramları, ikiden fazla sinüzoidi temsil etmek için çizilebilir.
Gerilim, akım veya başka bir değişken miktar olabilirler ancak hepsinin frekansı aynı olmalıdır.
Tüm fazörler saat yönünün tersine döndürülerek çizilir.
Referans fazörün önündeki tüm fazörlerin “öncü” olduğu söylenirken, referans fazlayıcının arkasındaki tüm fazörlerin “gecikme” olduğu söylenir.
Genel olarak, bir fazörün uzunluğunu rms maksimum değeri yerine sinüsoidal miktarın değeri olarak ifade edilir.
Farklı frekanslardaki sinüzoidler, vektörlerin farklı hızlarından dolayı aynı fazör diyagramında temsil edilemez.
Herhangi bir zamanda, aralarındaki faz açısı farklı olacaktır.İki veya daha fazla vektör birlikte eklenebilir veya çıkarılabilir ve Sonuç Vektörü adı verilen tek bir vektör olabilir.
Bir vektörün yatay tarafı gerçek veya “x” vektörüne eşittir. Bir vektörün dikey tarafı, hayali veya “y” vektörüne eşittir. Ortaya çıkan dik açılı üçgenin hipotenüsü “r” vektörüne eşdeğerdir.
Üç fazlı dengeli bir sistemde her bir fazör 120 derece ile yer değiştirmiştir.
FAZÖR DİYAGRAMLARI VE CEBİRİ NEDİR SONUÇ :
Bugün Fazör Diyagramları ve Cebiri Nedir adlı yazımızla karşınızdaydık.Bu diyagramlara , gösterim şekillerine ve matematiksel ifadelere dair birtakım bilgileri sizlerle paylaştık.
Umuyorum faydalı bilgiler edinmişsinizdir.
İyi Çalışmalar
